Question

There is a new diagnostic test for a disease that occurs in about 0.05% of the population. The test is not perfect, but will detect a person with the disease 99% of the time. It will, however, say that a person without the disease has the disease about 3% of the time. A person is selected at random from the population, and the test indicates that this person has the disease. What are the conditional probabilities that(a) the person has the disease? (b) the person does not have the disease?

Answer 1

(a) P(D|TD) = 0.0162 and (b) P(ND|TD) = 0.9838

Explanation:

Let's define the following events:

D: the person has the disease

ND: the person does not have the disease

TD: the test indicates the person has the disease. Then

P(D) = 0.0005 because the disease occurs in about 0.05% of the population.

P(ND) = 0.9995

P(TD|D) = 0.99 because the test detect a person with the disease 99% of the time.

P(TD|ND) = 0.03 because the test say that a person without the disease has the disease about 3% of the time.

We are looking for (a) P(D|TD) and (b) P(ND|TD)

By Bayes' formula

(a)
`P(D|TD) = (P(TD|D)P(D))/(P(TD|D)P(D)+P(TD|ND)P(ND)) = ((0.99)(0.0005))/((0.99)(0.0005)+(0.03)(0.9995))` =

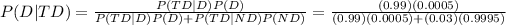0.0162

and

(b)
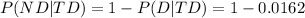`P(ND|TD) = 1-P(D|TD)=1-0.0162` = 0.9838