Question

A Coast Guard ship is traveling at a constant velocity of 4.25 m/s, due east, relative to the water. On his radar screen the navigator detects an object that is moving at a constant velocity. The object is located at a distance of 2315 m with respect to the ship, in a direction 31.0° south of east. Six minutes later, he notes that the object's position relative to the ship has changed to 1130 m, 57.5° south of west. What are the magnitude and direction of the velocity of the object relative to the water? Express the direction as an angle with respect to due west.

Answer 1

2.99 m/s north of west

Step-by-step explanation:

The first thing is to find the "north south" component of the displacement since the position of the coast guard ship doesn't change in that axis.

to find the y position on the first moment we can use the sine formula:

sin (a) = oposite side / hipotenuse

replacing and solving for y1 it would be

sin(31°) = y₁ / 2315m

y₁ = sin(31°)*2315m = 1192 m

that's how south of the coast guard ship the object is on the first moment

doing the same for the second moment we can get the y position for the second measurement

y₂ = sin(57.5°) * 1130 = 953 m

this means that in that time the object moved north 1192m - 953m = 176.96 m

_________

now to get the x component we do the same as before using cos and we'll get how far east the object is relative to the ship on the first moment

cos (31°) = x₁/ 2315m

x₁ = cos(31°) * 2315m = 1984 m (east)

now we do the same for x component for the ship on the second moment

cos(57.5°) * 1130 = 607m (west)

now to get these numbers on the same frame of reference to calculate.

the coast guard ship moved 4.25 m/s*60s*6 = 1530 m east.

This means that to get the x position for the object on the second moment *relative to where the coast guard ship was on the first moment*

we need to do

1530m - 607 m = 923m <--- THIS is our x₂

_______

so when we compare the x1 to x2 we see that the object moved 1984 m - 923m = 1061 m (west)

now to recap the object then moved (from its own original position)

176.96 meters north and 1061 meters west

now we have the two components of the movment

to get it's angle we use the inverse tangent (arctan,
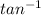`tan^(-1)`(x))

arctan(176.9/1061) = 9.46° north of west

for the speed we need the actual distance traveled, we can use pythagoras or any other trig function, in this case i'll use sin

sin(9.46°) = 176.9 / d

d = 176.9 / sin (9.86°) = 1076.3m

now dividing this distance with the seconds elapsed (60*6 = 360s)

we have that the final speed was

1076.3m

/360s= 2.9897 m/s north of west

(obviously depending on where you did the rounding it would get closer to 3)