Question

if f(x) = ax^6 + bx^4 + cx^3 where a,b, and c are integers, how many distinct rational zeros could f(x) have

Answer 1

You can rewrite your function as

`f(x) = x^3(ax^3+bx+c)`

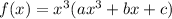
This implies that

`f(x)=0 \iff x^3=0\quad\lor\quad ax^3+bx+c=0`

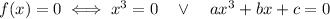
Now, we have
`x^3=0\iff x=0`, so it counts as a solution.

On the other hand, depending on the coefficient a, b and c, the cubic equation

`ax^2+bx+c=0`

can have either one or three solutions.

So, we have the solution x=0, and then one or three solutions coming from the cubic part. The equation as a whole thus have either two or four solutions, depending on the coefficients.