Answer:
24 units
Explanation:
The polygon with 5 vertices A (-2,1), B (-2, 4) , C (2, 7), D (6, 4) and E (6, 1).
where A
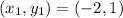 , B
, B
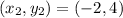
C
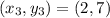 , D
, D
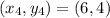
E
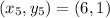
Now using distance formula:
Length of AB =
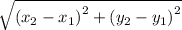
=
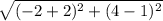
=
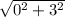
=
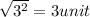
Length of BC =
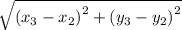
=
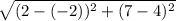
=
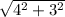
=
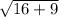
=
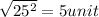
Length of CD =
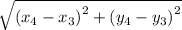
=
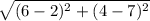
=
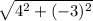
=
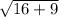
=
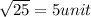
Length of DE =
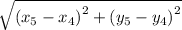
=
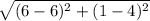
=
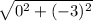
=
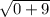
= 3 unit
Length of EA =
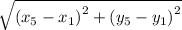
=
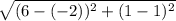
=
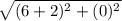
=
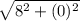
= 8 unit
Perimeter of polygon = Length of (AB + BC + CD + DE + EA)
= (3 + 5 + 5 + 3 + 8)
= 24 units