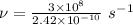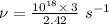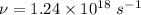Answer:
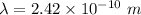
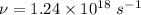
Step-by-step explanation:
The expression for the deBroglie wavelength is:

Where,
 is the deBroglie wavelength
is the deBroglie wavelength
h is Plank's constant having value

m is the mass of electron having value

v is the speed of electron.
Given that v = c / 100
Where, c is the speed of light having value
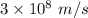
Thus, v =

Applying in the equation as:


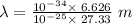
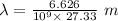
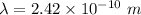
Also,
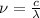
So,