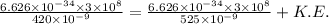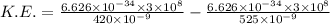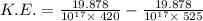Answer:

Step-by-step explanation:
Using the expression for the photoelectric effect as:
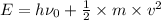
Also,
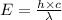
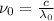
Applying the equation as:
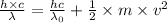
Where,
h is Plank's constant having value

c is the speed of light having value
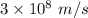
 is the wavelength of the light being bombarded
is the wavelength of the light being bombarded
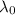 is the threshold wavelength
is the threshold wavelength
 is the kinetic energy of the electron emitted.
is the kinetic energy of the electron emitted.
Given,
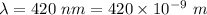

Thus, applying values as: