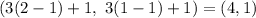Answer:
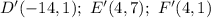
Explanation:
Since the center of dilation is not at the origin, we can use the following formula in order to find the coordinates of the vertices of the triangle D'E'F':

Where "O" is the center of dilation at (a,b) and "k" is the scale factor.
In this case you can identify that:
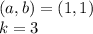
Therefore, susbtituting values into the formula shown above, you get that the coordinates ot the resulting triangle D'E'F, are the following:
Vertex D' →
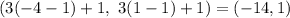
Vertex E' →

Vertex F' →