Step-by-step explanation:
According to Rydberg's formula, the wavelength of the balmer series is given by:
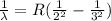
R is Rydberg constant for an especific hydrogen-like atom, we may calculate R for hydrogen and deuterium atoms from:
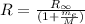
Here,
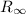 is the "general" Rydberg constant,
is the "general" Rydberg constant,
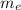 is electron's mass and M is the mass of the atom nucleus
is electron's mass and M is the mass of the atom nucleus
For hydrogen, we have,
 :
:
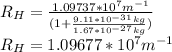
Now, we calculate the wavelength for hydrogen:
![(1)/(\lambda)=R_H((1)/(2^2)-(1)/(3^2))\\\lambda=[R_H((1)/(2^2)-(1)/(3^2))]^(-1)\\\lambda=[1.0967*10^7m^(-1)((1)/(2^2)-(1)/(3^2))]^(-1)\\\lambda=6.5646*10^(-7)m=656.46nm](https://img.qammunity.org/2020/formulas/physics/college/gun66xrdxbumnxg35n4wnd1l8myqhxrjmq.png)
For deuterium, we have
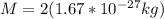 :
:
![R_D=(1.09737*10^7m^(-1))/((1+(9.11*10^(-31)kg)/(2*1.67*10^(-27)kg)))\\R_D=1.09707*10^7m^(-1)\\\\\lambda=[R_D((1)/(2^2)-(1)/(3^2))]^(-1)\\\lambda=[1.09707*10^7m^(-1)((1)/(2^2)-(1)/(3^2))]^(-1)\\\lambda=6.5629*10^(-7)=656.29nm](https://img.qammunity.org/2020/formulas/physics/college/ncci91y0gzsd1ev89au0s6xnsqj5md3c1m.png)