Question

A 100.0 g mass is placed on the meter stick 10.0 cm from the fulcrum. An unknown mass is positioned 3.0 cm from the fulcrum to balance the system. The mass of this unknown object is : (a) 0.11 kg (b) 0.22 kg (c) 0.33 kg (d) 0.44 kg

Answer 1

(c)0.33 Kg

Step-by-step explanation:

Hello

the two masses will generate a moment around the pivot point,

the generated moment is defined by

M=fxd

where f is the force and d is the distance,

now, for this case the force is the weight of the mass , it can be calculated by:

weight(w)=mg

where m is the acceleration of the gravity and m is the mass of the object.

the system is balanced so the two momentums are equal :

`M_(1)=M_(2)\\m_(1)*d_(1) *g=m_(2)*d_(2) *g\\the\ g\ is\ cancelled\\m_(1)*d_(1) =m_(2)*d_(2) \\isolating\ m_(2)\\`

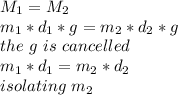
Let

`m_(1)=100\ g\\d_(1)=10\ cm\\d_(2)=3\ cm\\\\ replacing\\\\m_(2)=(m_(1)*d_(1) )/(d_(2))\\m_(2)=(100\ g*10\ cm )/(3\ cm)\\m_(2)=(1000\ g)/(3) \\m_(2)=333.33\ g\\`

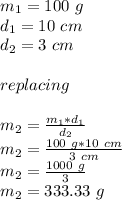
the answer is given in Kg, t

convert g into Kg using a rule of three

if

1Kg⇔ 1000 g

x?Kg ⇔ 333.33g

the relation is

`(1\ kg)/(1000\ g)= (x)/(333.33\ g)\\ solve \ for\ x \\x=(333.33\ g*1\ kg)/(1000\ g)\\x=(333.33 Kg)/(1000)\\ x=0.33\ Kg`

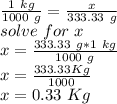
so, the answer is (c) 0.33 Kg

Have a good day