Answer:
- No, this doesn't mean the electric potential equals zero.
Step-by-step explanation:
In electrostatics, the electric field
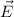 is related to the gradient of the electric potential V with :
is related to the gradient of the electric potential V with :
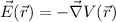
This means that for constant electric potential the electric field must be zero:
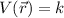
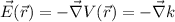
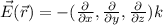
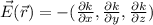

This is not the only case in which we would find an zero electric field, as, any scalar field with gradient zero will give an zero electric field. For example:

give an electric field of zero at point (0,0,0)