Answer:
A. Fnx = 5.71*10⁻⁵ N , Fny= -3.67*10⁻⁵ N
B. Fn= 6.78 *10⁻⁵ N
C. α= 32.4° counterclockwise with the positive x+ axis
Step-by-step explanation:
Because the particle q₃ is close to two other electrically charged particles, it will experience two electrical forces and the solution of the problem is of a vector nature.
Equivalences
1nC= 10⁻⁹C
1cm = 10⁻²m
Known data
k= 9*10⁹N*m²/C²
q₁= -2.65 nC =-2.65*10⁻⁹C
q₂= +2.00 nC = 2*10⁻⁹C
q₃= +5.00 nC= =+5*10⁻⁹C
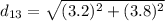
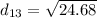 * 10⁻²m = 4.9678* 10⁻²m
* 10⁻²m = 4.9678* 10⁻²m
(d₁₃)² = 24.68*10⁻⁴m²
d₂₃ = 3.2 cm = 3.2*10⁻²m
Graphic attached
The directions of the individual forces exerted by q₁ and q₂ on q₃ are shown in the attached figure.
The force (F₂₃) of q₂ on q₃ is repulsive because the charges have equal signs and the forces.
The force (F₁₃) of q₁ on q₃ is attractive because the charges have opposite signs.
Magnitudes of F₁₃ and F₂₃
F₁₃ = (k*q₁*q₃)/(d₁₃)²=( 9*10⁹*2.65*10⁻⁹*5*10⁻⁹) /(24.68*10⁻⁴)
F₁₃ = 4.8 *10⁻⁵ N
F₂₃ = (k*q₂*q₃)/(d₂₃)² = ( 9*10⁹*2*10⁻⁹*5*10⁻⁹) /((3.2)²*10⁻⁴)
F₂₃ = 8.8 *10⁻⁵ N
x-y components of F₁₃ and F₂₃
F₁₃x= -4.8 *10⁻⁵ *cos β= - 4.8 *10⁻⁵(3.2/ (4.9678)= - 3.09*10⁻⁵ N
F₁₃y= -4.8 *10⁻⁵ *sin β= - 4.8 *10⁻⁵(3.8/(4.9678) = - 3.67*10⁻⁵ N
F₂₃x = F₂₃ = +8.8 *10⁻⁵ N
F₂₃y = 0
x and y components of the total force exerted on q₃ by q₁ and q₂ (Fn)
Fnx= F₁₃x+F₂₃x = - 3.09*10⁻⁵ N+8.8 *10⁻⁵ N= 5.71*10⁻⁵ N
Fny= F₁₃y+F₂₃y = - 3.67*10⁻⁵ N+0= - 3.67*10⁻⁵ N
Fn magnitude
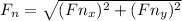
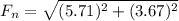 *10⁻⁵ N
*10⁻⁵ N
Fn= 6.78 *10⁻⁵ N
Fn direction (α)
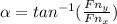
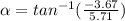
α= -32.4°
α= 32.4° counterclockwise with the positive x+ axis