Answer:
The slopes are different, and the y-intercepts are different.
Explanation:
From the graph:
Parallel lines have the same slope.
The lines are not parallel, therefore have the different slopes.
y-intercepts are different (look at the picture)
-1 and -8.
Answer:
The slopes are different, and the y-intercepts are different.
From the system of equations:
The slope-ntercept form of an equation of a line:

m - slope
b - y-intercept
We have the equations of a lines in the standard form (Ax + By = C).
Convert ot the slope-intercept form:
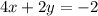 subtract 4x from both sides
subtract 4x from both sides
 divide both sides by 2
divide both sides by 2
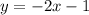
Therefore we have the slope m = -2, and the y-intercept b = -1.
 subtract x from both sides
subtract x from both sides
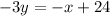 divide both sides by (-3)
divide both sides by (-3)
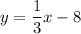
Therefore we have the slope m = 1/3, and the y-intercept b = -8.
-2 ≠ 1/3 and -1 ≠ -8
The slopes are different, and the y-intercepts are different.