Question

41. What is the velocity (speed AND direction) relative to Earth of a star with a spectral 1 normally seen at 625 nm that is now at 690 nm? (speed of light = 300,000 km/sec) A) 31,200 km/sec TOWARD Earth B) 31,200 km/sec AWAY from Earth C) 10.4 km/sec TOWARD Earth D) 10.4 km/sec AWAY from Earth

Answer 1

V = 31200000 m/s = 31200km/s

Step-by-step explanation:

when star recedes away from earth its wavelength will appear to increae

`(\Delta \lambda)/(\lambda_o) =(v)/(c)`

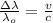
where c is speed of light

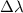`\Delta \lambda` is change in wavelength

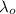`\lambda_o` is wavelength of star = 625 nm

therefore we have

solving for v

`v = (\Delta \lambda)/(c){\lamda_0}`

`v = ((690-625)* 10^(-9)* 3* 10^8)/(625* 10^(-9))`

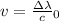
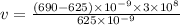
V = 31200000 m/s = 31200km/s