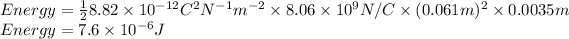Question

How much energy is stored by the electric field between two square plates, 6.1 cm on a side, separated by a 3.5 mm air gap? The charges on the plates are equal and opposite and of magnitude 530 μC. Express your answer using two significant figures

Answer 1

`7.6* 10^(-6) J`

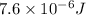
Step-by-step explanation:

The electric field between two plates is:

`E = (\sigma)/(2\epsilon)`

Where sigma is the superficial charge density and epsilon is the permittivity of air (is about the same as vaccum)

`\sigma = (Q)/(Area)= (530 * 10^(-6) C)/((0.061m)^2) = 0.14C/m^2`

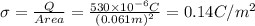
Using the formula to determine the electric field.

`E = (0.14C/m^2)/(2* 8.84 * 10^(-12)C^2N^(-1)m^(-2))\\E = 8.06 * 10^9 N/C`

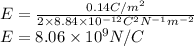
The energy inside the plates is given by the energy density due to electric Field times the volume:

`Energy = \rho_(E) * V = (1)/(2)\epsilon E V\\`

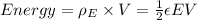
The volume is equal to the area of the plates times the distance between them:

`Energy = (1)/(2)8.82* 10^(-12)C^2 N^(-1)m^(-2) * 8.06 * 10^9 N/C * (0.061m)^2* 0.0035m\\Energy = 7.6 * 10^(-6) J`