Question

Express the following complex numbers in the form re (a) 4 3i (b) -2 -i

Answer 1

(a) 5 {Cos 37° + i Sin 37°}

(b) 2.24 {Cos 206.6° + i Sin 206.6°}

Step-by-step explanation:

(a) 4 + 3 i

Here it is written in standard form

Z = r (Cosθ + i Sinθ)

By comparison

r cosθ = 4

r sinθ = 3

Squarring both sides and then add

`r^(2)=4^(2)+3^(2)=25`

r = 5

By dividing

tanθ = 0.75

θ = 37°

So, it is written as 5 {Cos 37° + i Sin 37°}

(b) -2 - i

Here it is written in standard form

Z = r (Cosθ + i Sinθ)

By comparison

r cosθ = -2

r sinθ = - 1

Squarring both sides and then add

`r^(2)=(-2)^(2)+(-1)^(2)=5`

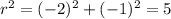
r = 2.24

By dividing

tanθ = 0.5

θ = 206.6°

So, it is written as 2.24 {Cos 206.6° + i Sin 206.6°}