Answer:
d=0.738cm
Step-by-step explanation:
We divide this problem in two parts, below the surface is part 1 (where we have
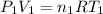 ), and on the surface part 2 (where we have
), and on the surface part 2 (where we have
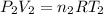 ). In this case, pressure, volume and temperature will vary, and n will remain constant because the amount of air is always the same (and R is always a constant), so we have
). In this case, pressure, volume and temperature will vary, and n will remain constant because the amount of air is always the same (and R is always a constant), so we have
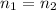 .
.
We can then do:
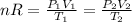
The volume of a sphere is
 , so we can write
, so we can write
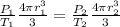
Which is
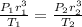
And obtain our radius for the bubble on the surface:
![r_2=\sqrt[3]{(P_1T_2r_1^3)/(P_2T_1)}=\sqrt[3]{(P_1T_2)/(P_2T_1)}r_1](https://img.qammunity.org/2020/formulas/physics/college/ees3grqssi10vx0mnugn3zamfq74tk9hgh.png)
Since the diameter is 2 times the radius this can be written as (the factor 2 cancels out):
![d_2=\sqrt[3]{(P_1T_2)/(P_2T_1)}d_1](https://img.qammunity.org/2020/formulas/physics/college/9ahwcjy41cv5rxesesvvt6wzqf1prcetuj.png)
And we put our values in S.I.:
![d_2=\sqrt[3]{((3atm)(298K))/((1atm)(278K))}(0.005m)=0.00738m=0.738cm](https://img.qammunity.org/2020/formulas/physics/college/rqo6mb8or0ozu4y6ikmyjhjtfmwfsk9r7v.png)