Step-by-step explanation:
It is given that,
Speed of the person, v = 3 mile/hr = 1.34 m/s
Speed of the truck, v' = 65 mile/hr = 29.05 m/s
(a) Since,
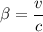
For the person,
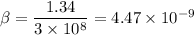
For the truck,
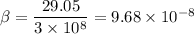
(b) The relativistic factor is given by :
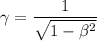
For very small velocity,
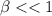
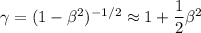
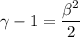
For the person :
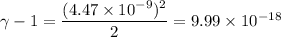
For the person :
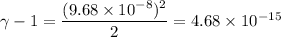
Hence, this is the required solution.