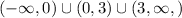Question

Find the domain of the following rational function.
8x(x-3)
F(x) =
2 - 7x-4

Answer 1

Domain is
`(-\infty, 0) \cup(0,3) \cup(3, \infty,)`

Solution:

As given in the problem, the rational function is,

`8 * x *(x-3) F(x)=2-7 x-4`

`F(x)=(-2-7 x)/(8 x(x-3))`

We know that the rational function is simply a fraction and in a fraction the denominator cannot be equal to zero because it would be undefined,

Hence from the equation above, we can say that

`F(x)=(-2-7 x)/(8 x(x-3))`

`8 x \\eq 0 \text { and }(x-3) \\eq 0`

`x \\eq 0 \text { and } x \\eq 3`

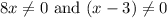
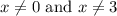
So, the domain is
`(- \infty, 0) \cup(0,3) \cup(3, \infty,)`