Answer:
The height of Mike’s new television is 32.32”
Solution:
Given that Mike’s new TV has diagonal measurement of 55” and length of 44.5’’.
We have to find the height of his new TV.
For a rectangle, relation between length, height and diagonal is given as,
 ---- eqn 1
---- eqn 1
As generally TV is rectangular shape, substituting the given dimensions in equation 1, we can find the height of his new TV
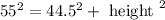
Rearranging the terms, we get
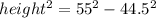
Taking square root on both sides, we get
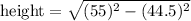
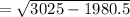

= 32.32”
Hence height of Mike’s new television is 32.32”.