Question

Consider the differential equation y' = y-t

a) construct a slope field for this equation

b) find the general solution to this differential equation

c) there is exactly one solution that is given by a straight line. write the equation for this line and draw it on the slope

Answer 1

The anwers are:

a) The slope field is attached.

b) The general solution is
`y(t)=c_(1)e^t+t+1`

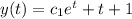
c) The solution that it is exactly a straight line is y(t)=t+1 (when c1=0)

Explanation:

y'(t)=y-t

y'(t)-y=-t

First we find the solution of the homogenous equaiton:

y'(t)-y=0

Considering
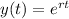`y(t)=e^(rt)` where r is a constant

`y'(t)=re^(rt)`

`re^(rt)-e^(rt)=0`

`(r-1)e^(rt)=0`

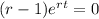
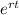`e^(rt)` is never zero, so:

(r-1)=0

r=1

`y(t)_(h)=c_(1)e^(t)`

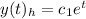
The particular solution is given by:

y(t)=At+B

y'(t)=A

Hence,

y'(t)-y=-t

A-At-B=-t

`\left \{ {{A-C=0} \atop {-A=-1}} \right.`

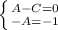
A=C=1

`y(t)_(p)=t+1`

The general solution is the sum of y(t)h and y(t)p:

`y(t)=c_(1)e^t+t+1`

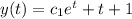
When c1=0, y(t)=t+1 which is a straight line of slope 1 and intercept 1.