Question

A loan of $100,000 is made today. The borrower will make equal repayments of $3568 per month with the first payment being exactly one month from today. The interest being charged on this loan is constant (but unknown).

For the following two scenarios, calculate the interest rate being charged on this loan, expressed as a nominal annual rate in percentage:

(b) The term of the loan is unknown but it is known that the loan outstanding 2 years later equals to $25044.84

Answer 1

The yearly interest rate is 5.20%.

Explanation:

This is a compound interest problem

The compound interest formula is given by:

`A = P(1 + (r)/(n))^(nt)`

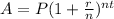
In which A is the amount of money, P is the principal(the initial sum of money), r is the interest rate(as a decimal value), n is the number of times that interest is compounded per unit t and t is the time the money is invested or borrowed for.

In this problem, we have that:

The loan outstanding is the value of the loan that has not been repaid.

Here, it is
`$25,044.84`.

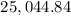To find the interest rate, we first have to find how much money the borrower will have to pay, that will be the value of A in the compound interest formula.

The total he will have to play is
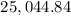`$25,044.84` plus the $3,568 he has already paid in each of the previous 2 years = 24 months. So:

`A = 25,044.84 + 24*3,568 = 110,676.84`.

P is the value of loan, so
`P = 100,000`

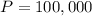
r is the interest rate, the value we have to find.

We have to find the annual interest rate, so
`n = 1`.

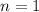We found the total amount in 2 years, so
`t = 2`.

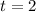Solving

`A = P(1 + (r)/(n))^(nt)`

`110,676.84 = 100,000(1 + r)^(2)`

`(1 + r)^(2) = 1.1067684`

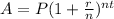
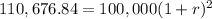
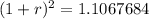
To find r, i will take the square root of both sides of the equation. So

`\sqrt{(1 + r)^(2)} = √(1.1067684)`

`1 + r = 1.0520`

`r = 0.0520`

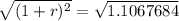
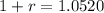
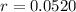
The yearly interest rate is 5.20%.