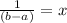Question

1/x+a=b, solve for x. im lost​

Answer 1

Explanation:

First, Let's take a on both sides:

`(1)/(x)+a-a=b-a`

`(1)/(x)=b-a`

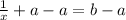
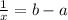
Remember that 1/x is called the reciprocal. For example the reciprocal of 2 is 1/2 and the reciprocal of 5 is 1/5. If we read the equation is telling us: "Reciprocal of x is b - a". Therefore,
`(1)/(b-a)=x`.

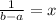Another way to solve it is to multiply x on both sides. Then,

`(x)/(x)=(b-a)*x`

`1=(b-a)*x`

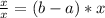
Then divide by (b-a). Remmebre to treat b-a as a factor:

`(1)/((b-a))=((b-a)*x)/((b-a))`

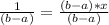
Cancelling (b-a) on the right hand side:

`(1)/((b-a))=x`