Question

Charcoal is found in a cave. It is determined that the amount of C – 14 present is 60% the amount when the wood was burned. If the C – 14 has a half-life of 5700 years, how long ago was the wood burned?

Answer 1

The wood was burned 4257 years ago.

Explanation:

The amount of C-14 present can be modeled by the following exponential function.

`C(t) = C_(0)e^(rt)`

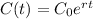
In which C is the amount remaining,
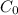`C_(0)` is the initial amount, r is the rate that the amount decrases, and t is the time in years.

The C – 14 has a half-life of 5700 years.

This means that

`C(5700) = 0.5C_(0)`

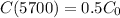
How long ago was the wood burned?

To solve this equation for t when
`C(t) = 0.6C_(0)`, the first step is finding the rate that the amount decreases. For this, we apply the half-life information in the equation.

First step: Find the rate that the amount of C-14 decreases.

`C(t) = C_(0)e^(rt)`

`0.5C_(0) = C_(0)e^(5700r)`

`e^(5700r) = 0.5`

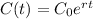
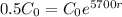
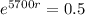
The next step here is applying ln, since ln and e are inverse functions.

`\ln{e^(5700r)} = ln(0.5)`

`5700r = -0.6931`

`r = (-0.6931)/(5700)`

`r = -0.00012`

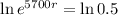
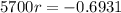
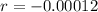
Final step: Find the time

We have that
`C(t) = 0.6C_(0)`,
`r = -0.00012`.

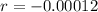So:

`C(t) = C_(0)e^(rt)`

`0.6C_(0) = C_(0)e^(-0.00012t)`

`e^(-0.00012t) = 0.6`

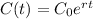
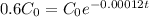
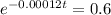
Applying the ln in both sides of the equality.

`\ln{e^(-0.00012t)} = ln(0.6)`

`-0.00012t = -0.5108`

`t = (0.5108)/(0.00012)`

`t = 4257`

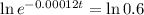
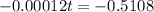
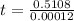
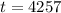
The wood was burned 4257 years ago.