Question

I am thinking of n consecutive positive integers, the smallest of which is m. What formula represents the largest of these integers?

Answer 1

`a_n=m+n-1`

Explanation:

We are given that n consecutive integers.

Smallest positive integer=m

We have to find the formula which represents the largest positive integer of given integers.

Suppose we have n positive consecutive integers

First integer=m

Second positive integer=m+1

Third integer=m+2

:

:

:

`d_1=m+1-m=1`

`d_2=m+2-m-1=1`

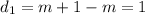
Difference between consecutive integers are constant. It means it is in A.P

nth term of AP is given by

`a_n=a+(n-1)d`

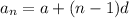
Substitute the value

`a_n=m+(n-1)`

`a_n=m+n-1`

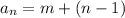
Hence, the formula that represents the largest integer of given integers is given by

`a_n=m+n-1`

Answer 2

`m+n-1`

Explanation:

I am thinking of n consecutive positive integers. The smallest of these numbers is m.

So,

• 
  `a_1=m` - the first number,
• 
  `a_2=m+1` - the second number,
• 
  `a_3=m+2` - the third number,
• ...
• 
  `a_n=m+(n-1)=m+n-1` - the nth number.

The list of n consecutive positive integers is

`m, \ m+1,\ m+2,\ m+3, \ ... ,\ m+n-1`

The largest integer is
`m+n-1`