Question

Let a, b, c, and d be real numbers with a, c 6= 0. Prove that the lines y = ax+b and y = cx + d have the same x-intercept if and only if ad = bc

Answer 1

Explanation:

We have got the lines :

`y=ax+b\\y=cx+d`

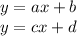
Both lines intercept the x-axis in the point :

`I = (i_(1) ,i_(2))`

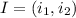
In all point from x-axis the y-component is equal to 0.

`I=(i_(1),o)`

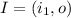
We replace the I point in the lines equations:

`0=a(i_(1))+b \\0=c(i_(1))+d`

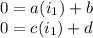
From the first equation :

`0=a(i_(1))+b \\-b=a(i_(1))\\i_(1)=(-b)/(a)`

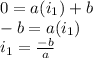
From the second equation :

`0=c(i_(1))+d\\ -d=c(i_(1))\\i_(1)=(-d)/(c)`

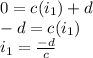
Then
`i_(1)=i_(1)`

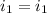
Finally :

`(-b)/(a)=(-d)/(c) \\(b)/(a)=(d)/(c) \\ad=bc`

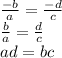
y = ax + b and y = cx + d have the same x-intercept ⇔ad=bc