Question

5. A tank initially contains 20 lb of salt dissolved in 200-gallon of water. Starting at time t = 0, a solution containing 0.5 lb of salt per gallon enters the tank at a rate of 4 gallons per minute and the well-stirred solution is withdrawn at the same rate. (a) Find the amount(in lb) of salt Q in the solution as a function of t in minutes. (b) Find the time at which the amount of salt in the tank reaches 50 lb. (c) Find the quantity of salt in the solution as t + .

Answer 1

(a) Amount of salt as a function of time

`A(t)=100-80e^(-0.02t)`

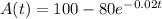
(b) The time at which the amount of salt in the tank reaches 50 lb is 23.5 minutes.

(c) The amount of salt when t approaches to +inf is 100 lb.

Explanation:

The rate of change of the amount of salt can be written as

`(dA)/(dt) =rate\,in\,-\,rate\,out\\\\(dA)/(dt)=C_i*q_i-C_o*q_o=C_i*q_i-(A(t))/(V)*q_o\\\\(dA)/(dt)=0.5*4-(A(t))/(200)*4\\\\(dA)/(dt) =(100-A(t))/(50)=-((A(t)-100)/(50))`

Then we can rearrange and integrate

`(dA)/(dt)= -((A(t)-100)/(50))\\\\\int (dA)/(A-100)=-(1)/(50)  \int dt\\\\ln(A-100)=-(t)/(50)+C_0\\\\ A-100=Ce^(-0.02*t)\\\\\\A(0)=20 \rightarrow 20-100=Ce^0=C\\C=-80\\\\A=100-80e^(-0.02t)`

Then we have the model of A(t) like

`A(t)=100-80e^(-0.02t)`

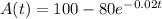
(b) The time at which the amount of salt reaches 50 lb is

`A(t)=100-80e^(-0.02t)=50\\\\e^(-0.02t)=(50-100)/(-80)=0.625\\\\-0.02*t=ln(0.625)=-0.47\\\\t=(-0.47)/(-0.02)=23.5`

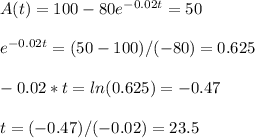
(c) When t approaches to +infinit, the term e^(-0.02t) approaches to zero, so the amount of salt in the solution approaches to 100 lb.