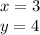Question

Use the Gauss-Jordan method to solve the following system of equations x+y 7 3x+2y= 17 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The solution is (Туре an ordered pair.) O B. There are infinitely many solutions. The solution is y, where y is any real number (Use integers or fractions for any numbers in the expression.) O C. The system is inconsistent

Answer 1

The system
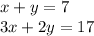`x+y=7\\3x+2y=17` has a unique solution
`x=3\\y=4`

Explanation:

We have the system of equations:

`x+y=7\\3x+2y=17`

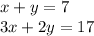
To solve this system for Gauss-Jordan method we need the augmented matrix, which is:

`\left[\begin{array}c1&1&7\\3&2&17\end{array}\right]`

Next we need to transform the augmented matrix to the reduced row echelon form via elementary row operations as follows:

• Row Operation 1: add -3 times the 1st row to the 2nd row

`\left[\begin{array}cc1&1&7\\0&-1&-4\end{array}\right]`

• Row Operation 2: multiply the 2nd row by -1

`\left[\begin{array}cc1&1&7\\0&1&4\end{array}\right]`

• Row Operation 3: add -1 times the 2nd row to the 1st row

`\left[\begin{array}cc1&0&3\\0&1&4\end{array}\right]`

From the reduced row echelon form we have the solution of the system

`x=3\\y=4`