Answer:
(q: 8,4,2,1)
q = 12
List all coalitions ( 2 pair)

Those whose total weight is equal to q or more than q will go further in the list of winning coalitions
So,
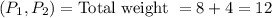 will go further in winning coalition
will go further in winning coalition
Coalitions ( 3 pair or more)
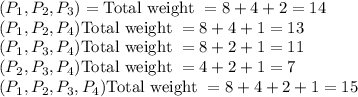
Those whose total weight is equal to q or more than q will go further in the list of winning coalitions
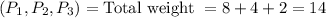

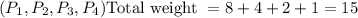
winning coalitions:
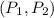
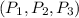
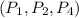
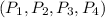
In case of
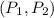
If Player 1 leaves
So, total weight will be 4
So, Player 1 is critical
If Player 2 leaves
So, total weight will be 8
So, Player 2 is critical
In case of
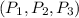
If Player 1 leaves
So, total weight will be 4+2=6
So, Player 1 is critical
If Player 2 leaves
So, total weight will be 8+2=10
So, Player 2 is critical
If Player 3 leaves
So, total weight will be 8+4=12
So, Player 3 is not critical since total weight is equal to q
In case of
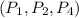
If Player 1 leaves
So, total weight will be 4+1=5
So, Player 1 is critical
If Player 2 leaves
So, total weight will be 8+1=9
So, Player 2 is critical
If Player 4 leaves
So, total weight will be 8+4=12
So, Player 4 is not critical since total weight is equal to q
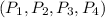
If Player 1 leaves
So, total weight will be 4+2+1=7
So, Player 1 is critical
If Player 2 leaves
So, total weight will be 8+2+1=11
So, Player 2 is critical
If Player 3 leaves
So, total weight will be 8+4+1=13
So, Player 3 is not critical since total weight is greater than q
If Player 4 leaves
So, total weight will be 8+4+2=14
So, Player 4 is not critical since total weight is greater than q
Player Times critical Banzhaf power index
1 4
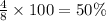
2 4
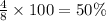
3 0 0
4 0 0
Sum = 8