Question

Solve the following differential equation: (2x+5y)dx+(5x−4y)dy=0 *Hint: they are exact

C=.

Answer 1

Answer with Step-by-step explanation:

The given differential equation is

`(2x+5y)dx+(5x-4y)dy=0`

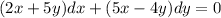
Now the above differential equation can be re-written as

`P(x,y)dx+Q(x,y)dy=0`

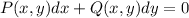
Checking for exactness we should have

`(\partial P)/(\partial y)=(\partial Q)/(\partial x)`

`(\partial P)/(\partial y)=(\partial (2x+5y))/(\partial y)=5`

`(\partial Q)/(\partial x)=(\partial (5x-4y))/(\partial x)=5`

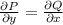
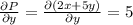
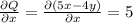
As we see that the 2 values are equal thus we conclude that the given differential equation is exact

The solution of exact differential equation is given by

`u(x,y)=\int P(x,y)dx+\phi(y)\\\\u(x,y)=\int (2x+5y)dx+\phi (y)\\\\u(x,y)=x^2+5xy+\phi (y)`

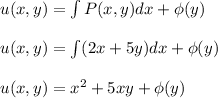
The value of
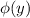`\phi (y)` can be obtained by differentiating u(x,y) partially with respect to 'y' and equating the result with P(x,y)

`(\partial u)/(\partial y)=(\partial (x^2+5xy+\phi (y))))/(\partial y)=Q(x,y))\\\\5y+\phi '(y)=(5x-4y)\\\\\phi '(y)=5x-9y\\\\\int\phi '(y)\partial y=\int (5x-9y)\partial y\\\\\phi (y)=5xy-(9y^2)/(2)\\\\\therefore u(x,y)=x^2+10xy-(9y^2)/(2)+c`