Answer:
a) According to the empirical rule, 99.7% of toner cartridges will print between 3282 and 5322 pages.
b) 95% of the toner cartridges have a print total between 3622 and 4982 pages.
c) The firm can expect to be responsible for replacing 5% of cartridges.
Explanation:
The mean number of pages a toner cartridge can print is 4302 and the standard deviation is 340, so
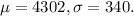
(a) Suppose a histogram of the data indicates that the sample data follow a bell-shaped distribution. According to the Empirical Rule, 99.7% of toner cartridges will print between
The Empirical Rule states that 99.7% of the values of X of a set with mean
 and standard deviation
and standard deviation
 belong to the following interval
belong to the following interval
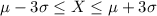
We have that
 .
.
So
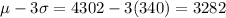

According to the empirical rule, 99.7% of toner cartridges will print between 3282 and 5322 pages.
(b) Assuming that the distribution of the data are bell. shaped, determine the percentage of toner cartridges whose print total is between 3622 and 4982 pages
How many standard deviations are those values from the mean?
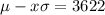
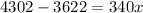
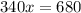
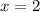
3622 pages is 2 standard deviations below the mean.
--------------

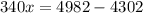
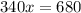
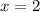
4982 pages is 2 standard deviations below the mean.
The Empirical Rule states that 95% of the values of X of a set with mean
 and standard deviation
and standard deviation
 belong to the following interval
belong to the following interval
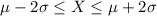
So, 95% of the toner cartridges have a print total between 3622 and 4982 pages.
(c) If the company that manufactures the toner cartridges guarantees to replace any cartridge that does not print at least 3622 pages, what percent of cartridges can the firm expect to be responsible for replacing, according to the Empirical Rule?
In b), we found that 3622 pages is 2 standard deviations below the mean.
The empirical rule states that 5% of the values are expected to be 2 standard deviations below the mean.
So, the firm can expect to be responsible for replacing 5% of cartridges.