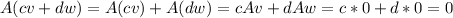Answer:
Let
 be an
be an
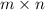 matrix and
matrix and
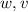 vectors in
vectors in
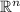 with the property that
with the property that
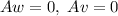 .
.
Then, using the distributive property between matrices we have that
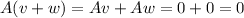 , so
, so
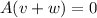
Now, let c and d scalars. Observe that using the property of product of a matrix by a scalar and the distributive property we have that