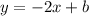Answer:
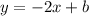
Explanation:
The equation of the given line is in slope-y_intercept form, so it is easy to see that the slope is "-2".
A parallel line to it should have the same slope. Therefore, it should have the form:
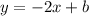
In order to determine the appropriate value of "b", we use the information that should pass through the point (-1,4) on the plane. That is when x = -1, the y-value must be "4".
We include this condition in the tentative equation of the parallel line we found above, and then solve for "b":
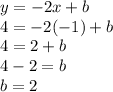
Therefore, the equation of the parallel line is: