Answer:
Explanation:
In this problem we are proving the equality
 .
.
When we want prove an equality by induction we need to follow some steps.
First: Check the hypothesis for some initial cases. In this exercise we take
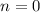 : we have
: we have
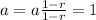 . So the equality holds for
. So the equality holds for
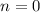 .
.
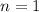 : we have
: we have
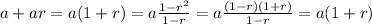 . So the equality holds for
. So the equality holds for
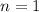 .
.
After we have checked the hypothesis for
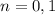 can continue to the next step.
can continue to the next step.
Second: State the induction hypothesis for
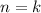 . In this case the hypothesis is:
. In this case the hypothesis is:
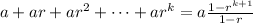 .
.
Now, it comes the last step and, usually, the most difficult.
Third: Prove the statement for
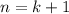 (using that the equality holds for
(using that the equality holds for
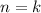 !). This means that we want to prove that:
!). This means that we want to prove that:
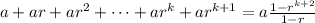 .
.
So, let us start by the left hand side and try to get the left hand side.
 .
.
We can group the above sum in the following way
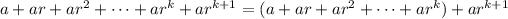 .
.
Notice that the expression under parenthesis is the same we have in our induction hypothesis. Then,
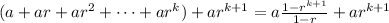 .
.
Now, we operate the sum that appears in the right hand side:
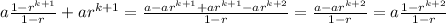 .
.
So, we have obtained that
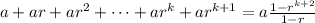 ,
,
which is exactly what we want to prove.