Question

Verify that |P(A)| = 2^n , if |A| = n for n = 0, 1, 2, 3.

Answer 1

We have to prove that,

|P(A)| =
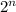`2^n` , if |A| = n for n = 0, 1, 2, 3.

For n = 0,

A = {}

P(A) = { {} } =
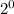`2^0` = 1

For n = 1,

A = { a } ( suppose )

P(A) = { {}, a } =
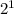`2^(1)` = 2,

For n = 2,

A = { a, b }

P(A) = { {}, {a}, {b}, {a, b} =
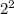`2^2` = 4,

For n = 3,

A = { a, b, c },

P(A) = { {}, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} } =
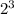`2^3` = 8

Thus, it is verified for n = 0, 1, 2, 3.

Now, suppose it is valid for a set B having k elements,

That is, |P(B)| =
`2^k`

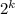
Also, there is a set A,

Such that, A = B ∪ {x}

Since, after including the element x in set B,

The element x will be come with every element of set B in the power set of B,

i.e. P(A) =
`2^k+2^k` =
`2^k(1+1)` =
`2^(k).2` =
`2^(k+1)`

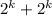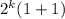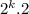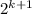
Hence, by the induction it has been proved,

|P(A)| =
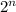`2^n` , if |A| = n, Where, n∈ N ( set of natural numbers )