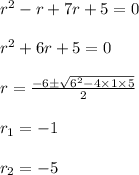Question

Let t^2y″+7ty′+5y=0.

Find all values of r such that y=t^r satisfies the differential equation for t>0.

If there is more than one correct answer, enter your answers as a comma separated list.

r=?

Answer 1

The values of r are -1 and -5.

Explanation:

Answer 2

The values of r are -1 and -5.

Explanation:

Since it is given that
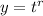`y=t^r` satisfy's the differential equation we put the 'y' in the equation and equate to 0

Also we have

`y'=(dt^r)/(dt)=rt^(r-1)\\\\y''=(d^(2)t^r)/(dt^2)\\\\y''=r(r-1)t^(r-2)`

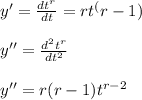
Using the values in the above equation we get

`t^2* r(r-1)t^(r-2)+7t* r* t^(r-1)+5t^(r)=0\\\\r(r-1)t^r+7rt^r+5t^r=0\\\\r(r-1)+7r+5=0.........(i)`

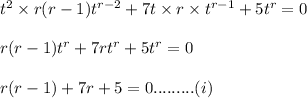
Since equation 'i' is a quadratic equation it is solved as under

`r^2-r+7r+5=0\\\\r^2+6r+5=0\\\\r=(-6\pm √(6^2-4* 1* 5) )/(2)\\\\r_1=-1\\\\r_2=-5`