Question

2. Solve the system of equations. Write your answer in parametric vector notation. X, +5x2 + 4x3 + 3x4 +9xs = 18 2x, +6x2 + 4x3 + 6x4 +6x3 = 28 3x, + 7x2 + 4xz +10x4 +lxs = 41 4x, + 6x2 + 2x3 +7x4 + 4x3 = 29

Answer 1

The system is inconsistent.

Explanation:

The system is

`x_1+5x_2+4x_3+3x_4+9x_5=18\\2x_1+6x_2+4x_3+6x_4+6x_5=28\\3x_1+7x_2+4x_3+10x_4+x_5=41\\4x_1+6x_2+2x_3+7x_4+4x_5=29`

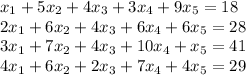
The associated matrix to the system is

`\left[\begin{array}{cccccc}1&5&4&3&9&18\\2&6&4&6&6&28\\3&7&4&10&1&41\\4&6&2&7&4&29\end{array}\right]`

Now we use row operations to find the echelon form of the matrix:

1. We substract to row 2, two times the row 1.

We substract to row 3, three times the row 1.

We substract to row 4, four times the row 1 and obtain the matrix

`\left[\begin{array}{cccccc}1&5&4&3&9&18\\0&-4&-4&0&-12&-8\\0&-8&-8&1&-26&-13\\0&-14&-14&-5&-32&-43\end{array}\right]`

2. We multiply the second row of the preview step by -1/4. We obtain the matrix

`\left[\begin{array}{cccccc}1&5&4&3&9&18\\0&1&1&0&3&2\\0&-8&-8&1&-26&-13\\0&-14&-14&-5&-32&-43\end{array}\right]`

3.

We add to row 3, eight times the row 2.

We add to row 4, fourtheen times the row 2 and obtain the matrix

`\left[\begin{array}{cccccc}1&5&4&3&9&18\\0&1&1&0&3&2\\0&0&0&1&-2&3\\0&0&0&-5&10&-155\end{array}\right]`

4. We add to row 4 of the preview step, five times the row 3 and obtain the matrix

`\left[\begin{array}{cccccc}1&5&4&3&9&18\\0&1&1&0&3&2\\0&0&0&1&-2&3\\0&0&0&0&0&-140\end{array}\right]`

Using backward substitution we have that

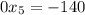`0x_5=-140`, then
`0=-140` and this is absurd. Then The system is inconsistent.