Answer:
The statement
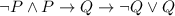 is a tautology.
is a tautology.
Explanation:
We have the following statement
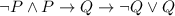
A truth table shows how the truth or falsity of a compound statement depends on the truth or falsity of the simple statements from which it's constructed.
The simple statements from the statement given are:
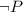 ,
,
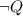 ,
,
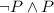 ,
,
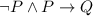 , and
, and
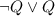 with these you can construct the following truth table.
with these you can construct the following truth table.
A tautology is a formula that is always true, it is true for every assignment of truth values to its simple components.
The last column contains only true values. Therefore, the statement is a tautology.