Question

Hunter invested $750 in an account paying an interest rate of 6\tfrac{5}{8}6 8 5 ​ % compounded continuously. London invested $750 in an account paying an interest rate of 6\tfrac{1}{2}6 2 1 ​ % compounded daily. After 18 years, how much more money would Hunter have in his account than London, to the nearest dollar?

Answer 1

Answer: $ 55

Explanation:

When interest is compounded continuously, the final amount will be

`A=Pe^(rt)`

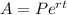
When interest is compounded daily, the final amount will be

`A=P(1+(r)/(365))^(365t)`

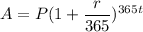
, where P= Principal , r = rate of interest , t = time

For Hunter , P= $750, r =
`6(5)/(8)\%=(53)/(8)\%=(53)/(800)=0.06625`

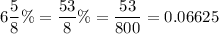
t = 18 years

`A=750e^(0.06625(18))=\$2471.48`

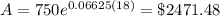
For London , P= $750, r =
`6(1)/(2)\%=(13)/(2)\%=\\eq (13)/(200)=0.065`

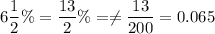
t = 18 years

`A=750(1+(0.065)/(365))^(18(365))=\$2416.24`

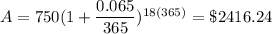
Difference = $ 2471.48 - $ 2416.24 =$ 55.24≈$ 55

Hence, Hunter would have $ 55 more than London in his account .