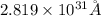Question

What is the length of a one-dimensional box for an electron (9.109 x 10-31 kg) with an n=1 energy of 479 kJ/mol? Give the answer in angstroms (A).

Answer 1

Answer : The length of a one-dimensional box for an electron is
`2.819* 10^(31)\AA`

Explanation :

The energy level of quantum particle in a one-dimensional box is given as:

`E_n=(n^2h^2)/(8mL^2)`

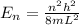
where,

`E_n` = 479 kJ/mol = 479000 J/mol

n = energy level = 1

h = Planck's constant =
`6.626* 10^(-34)Js`

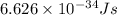
m = mass of electron =
`9.109* 10^(-31)kg`

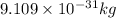
L = length of a one-dimensional box = ?

Now put all the given values in the above formula, we get:

`479000J/mol=((1)^2* (6.626* 10^(-34)Js)^2)/(8* (9.109* 10^(-31)kg)* L^2)`

`L=2.819* 10^(21)m`

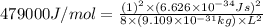
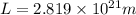
conversion used :
`1m=10^(10)\AA`

`L=2.819* 10^(31)\AA`

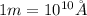
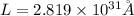
Therefore, the length of a one-dimensional box for an electron is
`2.819* 10^(31)\AA`