Question

A 1.00 cm2 blackbody surface emits 201 watts of radiant power. What is the temperature of the surface? Give to the nearest whole degree.

Answer 1

Step-by-step explanation:

Formula for black body radiation is as follows.

`(P)/(A) = \sigma * T^(4) J/m^(2)s`

where, P = power emitted

A = surface area of black body

`\sigma` = Stephen's constant =
`5.6703 * 10^(-8) watt/m^(2).K^(-4)`

As area is given as 1.0
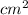`cm^(2)`. Converting it into meters as follows.

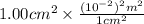`1.00 cm^(2) * ((10^(-2))^(2) m^(2))/(1 cm^(2))` (as 1 m = 100 cm)

=
`1 * 10^(-4) m^(2)`

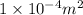
It is given that P = 201 watts. Hence,

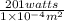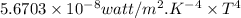
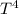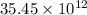
`(201 watts)/(1 * 10^(-4) m^(2))` =
`5.6703 * 10^(-8) watt/m^(2).K^(-4) * T^(4)`

`T^(4)` =
`35.45 * 10^(12)`

T =
`(35.45 * 10^(12))^(1/4)`

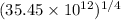
= 8862.5 K

Thus, we can conclude that the temperature of the surface is 8862.5 K.