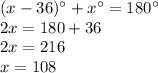Question

In the figure, AngleRQS Is-congruent-to AngleQLK. 3 lines are shown. Lines S P and K N are parallel. Line R M intersects line S P at point Q, and intersects line K N at point L. Angle R Q S is x degrees. Angle K L M is (x minus 36) degrees. What is the value of x?

Answer 1

x = 108

Explanation:

The attached image shows all the information given in the question.

`\angle RQS = \angle QLK\\SP \parallel KN\\\angle RQS=x\\\angle KLM= (x-36)`

We are given that

Angle RQS is congruent to Angle QLK

Thus, we can write:

`\angle QLK = x`

Since angle QLK and angle KLM forms a straight angle, we can write:

`\angle KLM + \angle QLK = 180^\circ\\x + (x-36) = 180\\2x - 36 = 180\\2x = 216\\x = 108`

Thus, x = 108

`\angle QLK= \angle RQS =108^\circ\\\angle KLM = 72^\circ`

Answer 2

x=108

Explanation:

see the attached figure to better understand the problem

we know that

m∠RQS≅m∠QLK -----> by corresponding angles

m∠KLM+m∠QLK=180° -----> by supplementary angles (consecutive interior angles)

we have that

m∠RQS=x° ----> given problem

so

m∠QLX=x°

m∠KLM=(x-36)° ----> given problem

substitute

`(x-36)\°+x\°=180\°\\2x=180+36\\2x=216\\x=108`