Answer:
A) The first 4 terms of the sequences are:
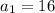 ,
,
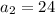 ,
,
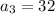 and
and
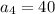 .
.
B) An explicit formula for this sequence can be written as:
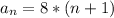
C) A recursive formula for this sequence can be written as:
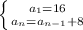
Explanation:
A) You can find the firs terms of this sequence simply selecting an odd integer and summing the consecutive 3 ones:
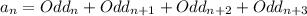 (a.1)
(a.1)
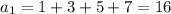
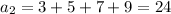
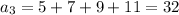
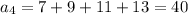
B) Observe the sequence of odd numbers 1, 3, 5, 7, 9, 11, 13(...).
You can express this sequence as:
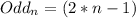 (b.1)
(b.1)
If you merge the expression b.1 in a.1, you obtain the explicit formula of the sequence:
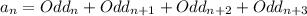 (a.1)
(a.1)
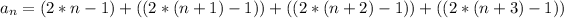 (b.2)
(b.2)
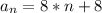 (b.3)
(b.3)
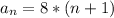 (b.s)
(b.s)
C) The recursive formula has to be written considering an initial term and an N term linked with the previous term. You can see an addition of 8 between a term and the next one. So you can express each term as an addition of 8 with the previous one. Therefore, if the first term is 16:
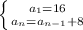 (c.s)
(c.s)