Answer:
(a)
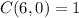 ,
,
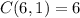 ,
,
 ,
,
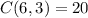 ,
,
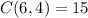 ,
,
 ,
,
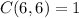 .
.
(b)
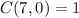 ,
,
 ,
,
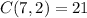 ,
,
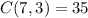 ,
,
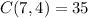 ,
,
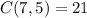 ,
,
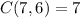 ,
,
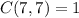 .
.
Explanation:
In this exercise we only need to recall the formula for C(n,k):
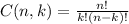
where the symbol
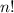 is the factorial and means
is the factorial and means
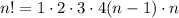 .
.
By convention 0!=1. The most important property of the factorial is
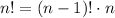 , for example 3!=1*2*3=6.
, for example 3!=1*2*3=6.
(a) The explanations to the solutions is just the calculations.
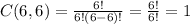 .
.
(b) The explanations to the solutions is just the calculations.
For all the calculations just recall that 4! =24 and 5!=120.