Answer:
The proof of this statement depends on the definition of closed set we are using. So, in the following explanation I will use that a subset
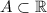 is closed if and only if it contains all its limit points.
is closed if and only if it contains all its limit points.
The first step is to prove the statement for
 . So, let us prove that if
. So, let us prove that if
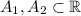 are closed, then
are closed, then
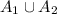 is closed.
is closed.
Fix
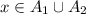 a limit point then, there exists a sequence
a limit point then, there exists a sequence
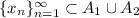 such that
such that
 .
.
Here we have three possibilities:
First: All the elements of
 are in
are in
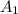 , except for a finite number of elements.
, except for a finite number of elements.
Second: All the elements of
 are in
are in
 , except for a finite number of elements.
, except for a finite number of elements.
Third: There are infinite elements of
 in
in
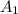 and in
and in
 .
.
In the first case we have that all the sequence, but a finite number of terms, is contained in
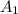 , which is closed. So, the limit of
, which is closed. So, the limit of
 is in
is in
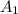 , hence
, hence
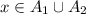 .
.
The second case has the same proof, just changing the indices 1 by 2.
The third case is less simpler. Let us call
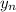 the part of
the part of
 that is contained in
that is contained in
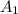 , and
, and
 the part of
the part of
 that is contained in
that is contained in
 . As every subsequence of a convergent sequence is also convergent, and to the same limit. So,
. As every subsequence of a convergent sequence is also convergent, and to the same limit. So,
 and
and
 .
.
Now, as
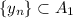 and
and
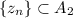 , and both sets are closed, we conclude that
, and both sets are closed, we conclude that
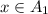 and
and
 , therefore
, therefore
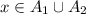 .
.
As the three options give us that
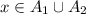 , we deduce that
, we deduce that
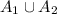 is closed.
is closed.
Finally, with a little inductive step we conclude that
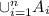 .
.
Explanation: