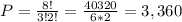Answer:
(a) 35 options
(b) 151,200 permutations
(c) 3,360 ways
Explanation:
a) The number of combinations of p=4 people out of a n=7 can be calculated as
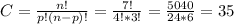
b) In this case is a permutation with no repetition of r=6 elements in a n=10 elements group.
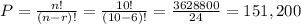
c) The word semester has 2 S's, 3 E's, 1 M, 1 T and 1 R (8 letters in total).
The total amount of permutations can be calculated as the total amount of permutations of letters, divided by the factorial of the amount of times a same letter repeats in the word. Or is the same to say, dividing by the amount of repetitions of the same permutation.