Answer:
The 10th term of the G.P is 29.
Explanation:
Given : In a GP if
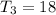 and
and
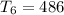 .
.
To find : The term
 ?
?
Solution :
The geometric sequence is in the form,
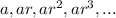
Where, a is the first term and r is the common ratio.
The nth term of G.P is
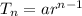
We have given,
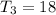
i.e.
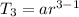
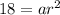 ....(1)
....(1)
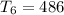
i.e.
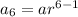
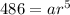 ....(2)
....(2)
Solving (1) and (2) by dividing them,
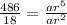
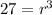
![r=\sqrt[3]{27}](https://img.qammunity.org/2020/formulas/mathematics/high-school/lzfrvh1jgfchsqu6oi5pwe9zoa76mpchb7.png)
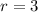
Substitute in (1),

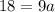
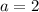
The first term is a=2 and the common ratio is r=3.
The 10th term, of GP is given by,
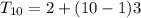
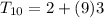
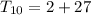
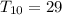
Therefore, The 10th term of the G.P is 29.