Answer:
1. We have the complex map
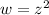 which transform the plane
which transform the plane
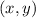 to the plane
to the plane
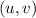 . This is
. This is
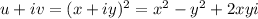 .
.
Now, the complex numbers on the line
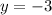 are of the form
are of the form
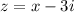 . if we substitute those values into the map we get
. if we substitute those values into the map we get
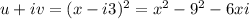 .
.
So,
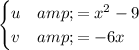 .
.
This means that we can consider the above equation as the parametric equation of the image of the line
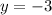 by the map
by the map
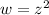 .
.
It is not difficult to notice that this is the parametric equation of a parabola. In order to obtain its Cartesian equation in the plane
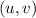 we only need to "eliminate" the parameter
we only need to "eliminate" the parameter
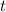 . This can be done by the following relation:
. This can be done by the following relation:
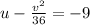
that gives the Cartesian equation
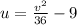 . In the usual
. In the usual
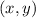 coordinates we have the equation
coordinates we have the equation
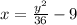 .
.
In the attached figure we have its graph.
2. From the parametric equation we can see that if
 moves from
moves from
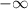 to
to
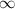 the image point moves from the branch of the parabola situated on the first quadrant crossing the horizontal axis when
the image point moves from the branch of the parabola situated on the first quadrant crossing the horizontal axis when
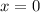 and then going through the branch on the fourth quadrant to infinity.
and then going through the branch on the fourth quadrant to infinity.