Question

Find a solution to y'(t) = te^-t satisfying the condition y(1) = 1.

Answer 1

`y=-e^(-t)(t+1)+1+(2)/(e)`

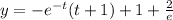
Explanation:

The given differential equation is

`y'(t)=te^(-t)`

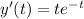
It can be written as

`(dy)/(dt)=te^(-t)`

`dy=te^(-t)dt`

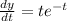
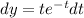
Integrate both sides.

`\int dy=\int te^(-t)dt`

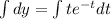
Apply ILATE rule on right side. Here, t is first function and
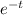`e^(-t)` is the second function.

`y=t\int e^(-t)-\int ((d)/(dt)t\int e^(-t))`

`y=-te^(-t)-\int (1* (-e^(-t)))`
`\int e^(-x)=-e^(-x)+C`

`y=-te^(-t)+\int e^(-t)`

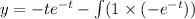
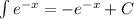
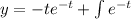
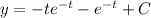`y=-te^(-t)-e^(-t)+C` .... (1)

Initial condition is y(1) = 1. It means at t=1 the value of y is 1.

`1=-(1)e^(-t)-e^(-(1))+C`

`1=-e^(-1)-e^(-1)+C`

`1=-2e^(-1)+C`

`1=-(2)/(e)+C`

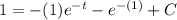
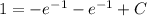
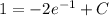
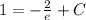
Add
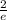`(2)/(e)` on both sides.

`1+(2)/(e)=C`

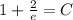
Substitute the value of C in equation (1).

`y=-te^(-t)-e^(-t)+1+(2)/(e)`

`y=-e^(-t)(t+1)+1+(2)/(e)`

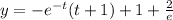
Therefore, the solution of given initial value problem is
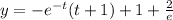`y=-e^(-t)(t+1)+1+(2)/(e)`.