Answer:
The statement
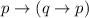 is a tautology.
is a tautology.
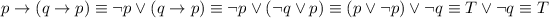
Explanation:
We have the following statement:
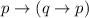
To reduce the statement to a tautology we need to use the table of logical equivalences as follows:
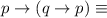
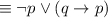 by the the logical equivalence involving conditional statement.
by the the logical equivalence involving conditional statement.
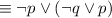 by the the logical equivalence involving conditional statement.
by the the logical equivalence involving conditional statement.
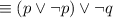 by the Associative law.
by the Associative law.
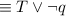 by the Negation law.
by the Negation law.
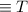 by the Domination law.
by the Domination law.