Answer:
The Fourier series of f(x) converges to 3 at the points x= π+2kπ, where k is an integer.
Explanation:
First, recall that the function f(x) is extended 2π periodic to the whole real line, in order to obtain a valid Fourier expansion. Remember that a Fourier series is formed by a sines and cosines, which are 2π-periodic.
So, the 2π-periodic expansion of f(x) is discontinuous at the points π+2kπ, in particular π and -π. Check the attached figure to a better understanding.
Now, the Dirichlet theorem on the convergence of a Fourier series tells us that the series converges to the function at the points of continuity, and at points of discontinuity the sum of the series is
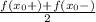 .
.
Here we understand the notation
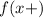 and
and
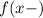 as
as
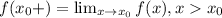
and
 .
.
In this particular case
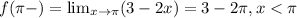 .
.
For the limit
 , with
, with
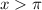 recall that our function is 2π-periodic, so the values of f near π, with x>π are the same when x is near -π and x>-π. Again, check the attached figure. So,
recall that our function is 2π-periodic, so the values of f near π, with x>π are the same when x is near -π and x>-π. Again, check the attached figure. So,
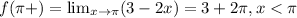 .
.
Thus,
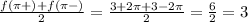 .
.
Note: In the attached figure we only have drawn three repetitions of the 2π-periodic extension of
 , recall that the extension is ad infinitum. Also, the points drawn in the dotted lines are the sum of the series at the points of discontinuity.
, recall that the extension is ad infinitum. Also, the points drawn in the dotted lines are the sum of the series at the points of discontinuity.